Overview
This project is a comprehensive exploration of various mathematical curves implemented using C# and the .NET Framework. The demo showcases how different mathematical concepts and algorithms can be applied to generate, manipulate, and visualize curves. The primary focus is on Polynomial Functions, Bezier Curves, Interpolating Polynomials, and B-Spline.
Polynomial Functions
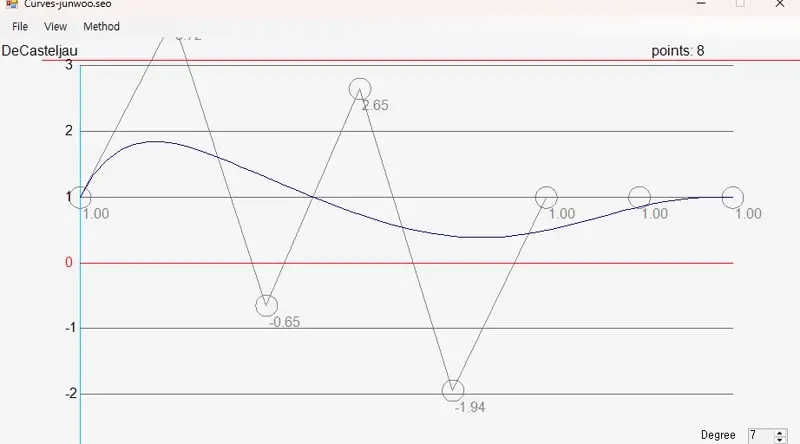
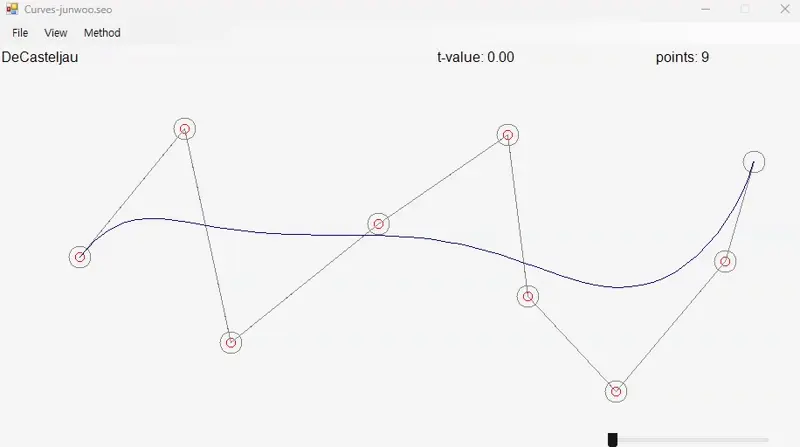
De Casteljau’s algorithm is a recursive approach to evaluate Bezier curves, which is crucial for constructing polynomial curves. In this demo, the algorithm is implemented to demonstrate how changing control points influences the curve’s shape.
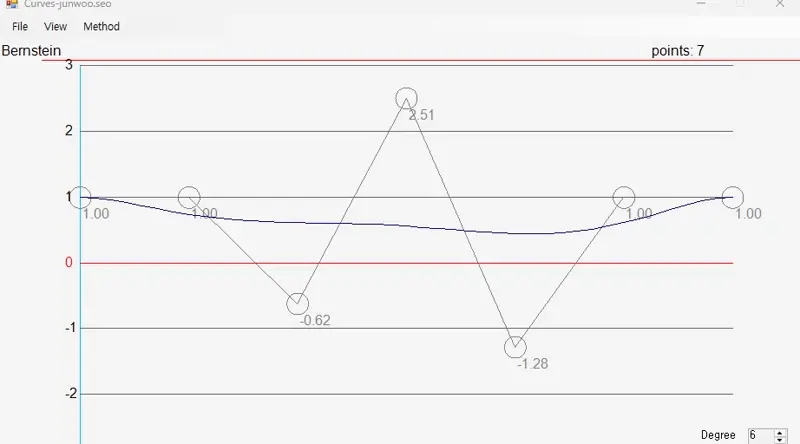
Bernstein polynomials form the basis functions for Bezier curves. They are used to construct the polynomial by blending control points according to specific weightings determined by the polynomials. This method provides a direct and mathematically elegant way to generate Bezier curves
Bezier Curves
Bernstein Method
The Bernstein method uses the polynomials described above to construct Bezier curves. This method emphasizes the mathematical foundation of Bezier curves, where the curve is expressed as a weighted sum of control points.
De Casteljau’s Algorithm
This algorithm provides a geometric approach to constructing Bezier curves. It is particularly useful for breaking down the curve construction into intuitive steps, making the curve easier to understand and visualize. through De Casteljau’s recursive process we can drive Midpoint Subdivision process.
Midpoint Subdivision
Midpoint Subdivision is a technique used to refine a curve by recursively subdividing it into smaller segments. This method is particularly effective for rendering high-precision curves or when dealing with large datasets where curve approximation is necessary
Interpolations
Interpolating Polynomials
Developed interpolating polynomials that pass through a given set of points, showcasing their effectiveness in curve fitting and data approximation.
Interpolating Cubic Splines
Implemented cubic splines to create smooth, continuous curves that interpolate a series of points. This technique ensures both first and second derivatives are continuous, resulting in smooth transitions between curve segments.
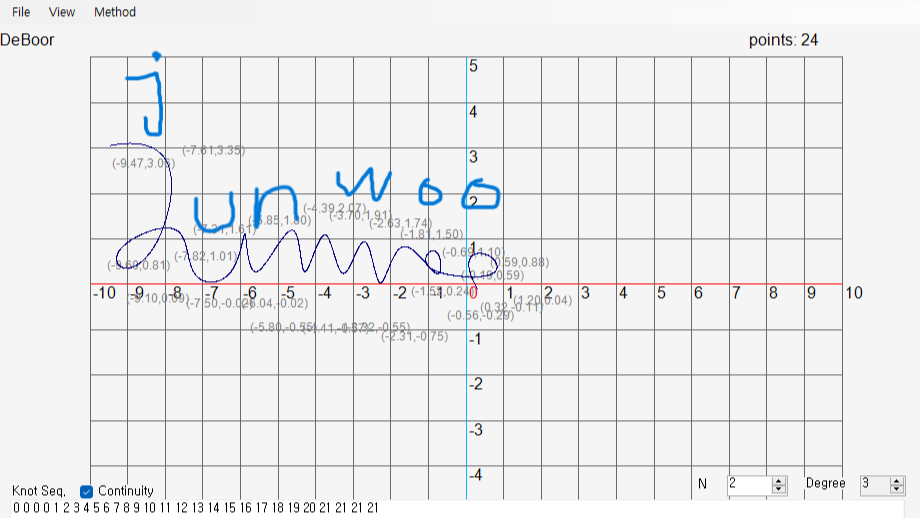
De Boor Algorithm for B-Spline Curves
Applied De Boor’s algorithm for B-Spline curve generation. This method is particularly effective for creating flexible and smooth curves that do not necessarily pass through their control points.
Results
The demo effectively visualizes the mathematical principles behind each curve generation technique. By allowing real-time manipulation of control points and parameters, the project highlights the differences and advantages of each method, providing users with a comprehensive understanding of curve behavior and properties. The interactive interface also showcases the efficiency of the algorithms, as the curves are recalculated and rendered dynamically.
